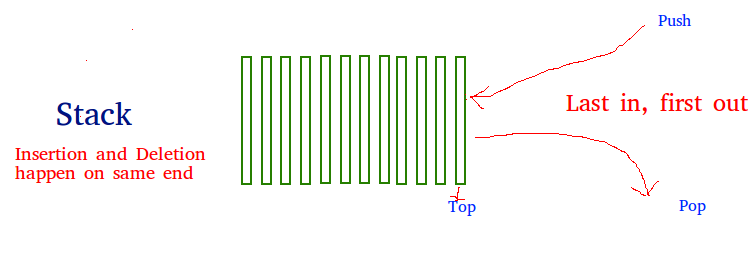
Stack Data Structure
INTRODUCTION
Stack is a linear data structure which follows a particular order in which the operations are performed. The order may be LIFO(Last In First Out) or FILO(First In Last Out).
There are many real-life examples of a stack. Consider an example of plates stacked over one another in the canteen. The plate which is at the top is the first one to be removed, i.e. the plate which has been placed at the bottommost position remains in the stack for the longest period of time. So, it can be simply seen to follow LIFO(Last In First Out)/FILO(First In Last Out) order
There are two operations in the stack: -
1. Push
2. Pop
When an item is inserted in the stack it is called push operation and when the item is
deleted in the stack it is called pop operation.
Mainly stack has two condition:
1. Overflow
2. Underflow
Overflow: This condition of stack occurred when stack is completely filled even we try to
push an element into it.
Underflow: This condition of stack occurred when stack is completely empty again we try to pop some element from it.
Basically, we can call a stack as overflow when it is completely filled and then underflow
when it is completely empty.
 A queue has two ends, one is the front end and the other is the rear end. The item is added to the rear end and the item is removed from the front end.
A queue has two ends, one is the front end and the other is the rear end. The item is added to the rear end and the item is removed from the front end.
There are mainly two basic operations of Queue:
I. Enqueue
II. Dequeue
When we insert an item in Queue, that process is called Enqueue and when we remove an item from Queue, that process is called Dequeue
Representation of stacks and queues using arrays:
In array implementation, the stack is formed by using the array. All the operation regarding the stack are performed using arrays. Let's see how each operation can be implemented on the stack using array data structure.
Adding an element onto the stack (push operation)
Adding an element into the top of the stack is referred to as push operation. Push operation involves the following two steps.
1. Increment the variable Top so that it can now refer to the next memory location.
2. Add element at the position of incremented top. This is referred to as adding a new element at the top of the stack.
The stack is overflown when we try to insert an element into a completely filled stack therefore, our main function must always avoid stack overflow condition.
Algorithm:
Start
if top = n then stack full
top = top + 1
stack (top): = item;
end
Time Complexity: o(1)
Implementation of push algorithm in C language:
void push (int val,int n) //n is size of the stack
{
if (top == n)
printf("\n Overflow");
else
{
top = top +1;
stack[top] = val;
}
}
Deletion of an element from a stack (Pop operation)
Deletion of an element from the top of the stack is called pop operation. The value of the variable top will be incremented by 1 whenever an item is deleted from the stack. The topmost element of the stack is stored in another variable and then the top is decremented by 1. The operation returns the deleted value that was stored in another variable as the result.
The underflow condition occurs when we try to delete an element from an already empty stack.
Algorithm :
begin
if top = 0 then stack empty;
Item: = stack (top);
top = top - 1;
end;
Implementation of the POP algorithm using C language:
int pop ()
{
if(top == -1)
{
printf("Underflow");
return 0;
}
else
{
return stack[top - - ];
}
}
Visiting each element of the stack (Peek operation)
Peek operation involves returning the element which is present at the top of the stack without deleting it. Underflow condition can occur if we try to return the top element in an already empty stack.
Algorithm :
PEEK (STACK, TOP)
Begin
If top = -1 then stack empty
Item = stack [top]
return item
End
Time complexity: o(n)
Implementation of Peek algorithm in C language:
int peek()
{
if (top == -1)
{
printf("Underflow");
return 0;
}
else
{
return stack [top];
}
}
C program:
#include
int stack[100],i,j,choice=0,n,top=-1;
void push();
void pop();
void show();
void main ()
{
printf("Enter the number of elements in the stack ");
scanf("%d",&n);
printf("*********Stack operations using array*********");
printf("\n----------------------------------------------\n");
while(choice != 4)
{
printf("Chose one from the below options...\n");
printf("\n1.Push\n2.Pop\n3.Show\n4.Exit");
printf("\n Enter your choice \n");
scanf("%d",&choice);
switch(choice)
{
case 1:
{
push();
break;
}
case 2:
{
pop();
break;
}
case 3:
{
show();
break;
}
case 4:
{
printf("Exiting....");
break;
}
default:
{
printf("Please Enter valid choice ");
}
};
}
}
void push ()
{
int val;
if (top == n )
printf("\n Overflow");
else
{
printf("Enter the value?");
scanf("%d",&val);
top = top +1;
stack[top] = val;
}
}
void pop ()
{
if(top == -1)
printf("Underflow");
else
top = top -1;
}
void show()
{
for (i=top;i>=0;i--)
{
printf("%d\n",stack[i]);
}
if(top == -1)
{
printf("Stack is empty");
}
}
Stack using Linked List:
Implementation of Stack using Linked List:
Stacks can be easily implemented using a linked list. Stack is a data structure to which data can be added using the push() method and data can be removed from it using the pop() method. With a Linked list, the push operation can be replaced by the add At Front() method of linked list and pop operation can be replaced by a function that deletes the front node of the linked list.
In this way, our Linked list will virtually become a Stack with push() and pop() methods.
First, we create a class node. This is our Linked list node class which will have data in it and a node pointer to store the address of the next node element.
class node
{
int data;
node *next;
};
Then we define our stack class,
class Stack
{
node *front; // points to the head of list
public:
Stack()
{
front= NULL;
}
// push method to add data element
void push(int);
// pop method to remove data element
void pop(); // top method to return top data element
int top();
};
Inserting Data in Stack (Linked List)
In order to insert an element into the stack, we will create a node and place it in front of the list:
void Stack :: push(int d)
{
// creating a new node
node *temp;
temp = new node();
// setting data to it
temp->data = d;
// add the node in front of list if(front == NULL) { temp->next = NULL; }
else
{
temp->next = front;
}
front = temp;
}
Now, whenever we will call the push() function a new node will get added to our list in the front, which is exactly how a stack behaves.
Removing Element from Stack (Linked List)
In order to do this, we will simply delete the first node, and make the second node, the head of the list.
void Stack :: pop()
{
// if empty
if(front == NULL)
cout << "UNDERFLOW\n";
// delete the first element
else
{
node *temp = front;
front = front->next;
delete(temp);
}
}
Return Top of Stack (Linked List)
In this, we simply return the data stored in the head of the list,
Int Stack : top ()
{
return front->data;
}
Conclusion:
When we say "implementing Stack using Linked List", we mean how we can make a Linked List behave like a Stack, after all, they are all logical entities. So for any data structure to act as a Stack, it should have push() method to add data on the top and pop() method to remove data from the top. Which is exactly what we did and hence accomplished to make a Linked List behave as a Stack.
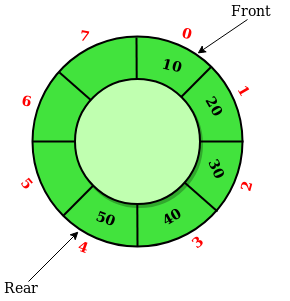
Circular queues
Circular Queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle and the last position is connected back to the first position to make a circle. It is also called ‘Ring Buffer’
Enqueue- adding an element in the queue if there is space in the queue.
Dequeue- Removing elements from a queue if there are any elements in the queue
Front- get the first item from the queue.
Rear- get the last item from the queue.
isEmpty/isFull- checks if the queue is empty or full
Applications of a Circular Queue
Memory management: circular queue is used in memory management.
Process Scheduling: A CPU uses a queue to schedule processes.
Traffic Systems: Queues are also used in traffic systems
Priority Queue
The priority queue is that in which there is an extension of the queue. This is a type of special data structure.
Example
1. Push
2. Pop
When an item is inserted in the stack it is called push operation and when the item is
deleted in the stack it is called pop operation.
Mainly stack has two condition:
1. Overflow
2. Underflow
Overflow: This condition of stack occurred when stack is completely filled even we try to
push an element into it.
Underflow: This condition of stack occurred when stack is completely empty again we try to pop some element from it.
Basically, we can call a stack as overflow when it is completely filled and then underflow
when it is completely empty.
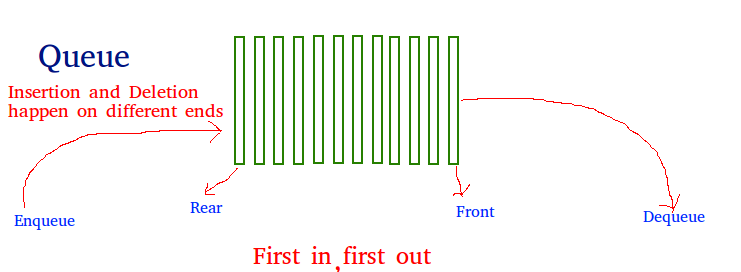
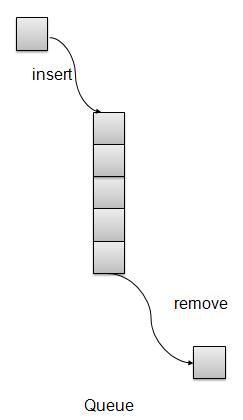
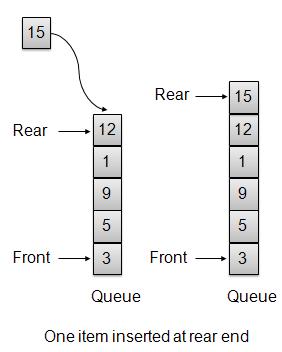
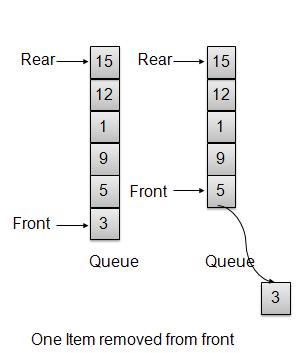
Queue Data Structure
INTRODUCTION
A Queue is a linear structure which follows a particular order in which the operations are performed. The order is First In First Out (FIFO). A good example of a queue is any queue of consumers for a resource where the consumer that came first is served first. The difference between stacks and queues is in removing. In a stack we remove the item the most recently added; in a queue, we remove the item the least recently added.

There are mainly two basic operations of Queue:
I. Enqueue
II. Dequeue
When we insert an item in Queue, that process is called Enqueue and when we remove an item from Queue, that process is called Dequeue
Representation of stacks and queues using arrays:
In array implementation, the stack is formed by using the array. All the operation regarding the stack are performed using arrays. Let's see how each operation can be implemented on the stack using array data structure.
Adding an element onto the stack (push operation)
Adding an element into the top of the stack is referred to as push operation. Push operation involves the following two steps.
1. Increment the variable Top so that it can now refer to the next memory location.
2. Add element at the position of incremented top. This is referred to as adding a new element at the top of the stack.
The stack is overflown when we try to insert an element into a completely filled stack therefore, our main function must always avoid stack overflow condition.
Algorithm:
Start
if top = n then stack full
top = top + 1
stack (top): = item;
end
Time Complexity: o(1)
Implementation of push algorithm in C language:
void push (int val,int n) //n is size of the stack
{
if (top == n)
printf("\n Overflow");
else
{
top = top +1;
stack[top] = val;
}
}
Deletion of an element from a stack (Pop operation)
Deletion of an element from the top of the stack is called pop operation. The value of the variable top will be incremented by 1 whenever an item is deleted from the stack. The topmost element of the stack is stored in another variable and then the top is decremented by 1. The operation returns the deleted value that was stored in another variable as the result.
The underflow condition occurs when we try to delete an element from an already empty stack.
Algorithm :
begin
if top = 0 then stack empty;
Item: = stack (top);
top = top - 1;
end;
Implementation of the POP algorithm using C language:
int pop ()
{
if(top == -1)
{
printf("Underflow");
return 0;
}
else
{
return stack[top - - ];
}
}
Visiting each element of the stack (Peek operation)
Peek operation involves returning the element which is present at the top of the stack without deleting it. Underflow condition can occur if we try to return the top element in an already empty stack.
Algorithm :
PEEK (STACK, TOP)
Begin
If top = -1 then stack empty
Item = stack [top]
return item
End
Time complexity: o(n)
Implementation of Peek algorithm in C language:
int peek()
{
if (top == -1)
{
printf("Underflow");
return 0;
}
else
{
return stack [top];
}
}
C program:
#include
int stack[100],i,j,choice=0,n,top=-1;
void push();
void pop();
void show();
void main ()
{
printf("Enter the number of elements in the stack ");
scanf("%d",&n);
printf("*********Stack operations using array*********");
printf("\n----------------------------------------------\n");
while(choice != 4)
{
printf("Chose one from the below options...\n");
printf("\n1.Push\n2.Pop\n3.Show\n4.Exit");
printf("\n Enter your choice \n");
scanf("%d",&choice);
switch(choice)
{
case 1:
{
push();
break;
}
case 2:
{
pop();
break;
}
case 3:
{
show();
break;
}
case 4:
{
printf("Exiting....");
break;
}
default:
{
printf("Please Enter valid choice ");
}
};
}
}
void push ()
{
int val;
if (top == n )
printf("\n Overflow");
else
{
printf("Enter the value?");
scanf("%d",&val);
top = top +1;
stack[top] = val;
}
}
void pop ()
{
if(top == -1)
printf("Underflow");
else
top = top -1;
}
void show()
{
for (i=top;i>=0;i--)
{
printf("%d\n",stack[i]);
}
if(top == -1)
{
printf("Stack is empty");
}
}
Stack using Linked List:
Implementation of Stack using Linked List:
Stacks can be easily implemented using a linked list. Stack is a data structure to which data can be added using the push() method and data can be removed from it using the pop() method. With a Linked list, the push operation can be replaced by the add At Front() method of linked list and pop operation can be replaced by a function that deletes the front node of the linked list.
In this way, our Linked list will virtually become a Stack with push() and pop() methods.
First, we create a class node. This is our Linked list node class which will have data in it and a node pointer to store the address of the next node element.
class node
{
int data;
node *next;
};
Then we define our stack class,
class Stack
{
node *front; // points to the head of list
public:
Stack()
{
front= NULL;
}
// push method to add data element
void push(int);
// pop method to remove data element
void pop(); // top method to return top data element
int top();
};
Inserting Data in Stack (Linked List)
In order to insert an element into the stack, we will create a node and place it in front of the list:
void Stack :: push(int d)
{
// creating a new node
node *temp;
temp = new node();
// setting data to it
temp->data = d;
// add the node in front of list if(front == NULL) { temp->next = NULL; }
else
{
temp->next = front;
}
front = temp;
}
Now, whenever we will call the push() function a new node will get added to our list in the front, which is exactly how a stack behaves.
Removing Element from Stack (Linked List)
In order to do this, we will simply delete the first node, and make the second node, the head of the list.
void Stack :: pop()
{
// if empty
if(front == NULL)
cout << "UNDERFLOW\n";
// delete the first element
else
{
node *temp = front;
front = front->next;
delete(temp);
}
}
Return Top of Stack (Linked List)
In this, we simply return the data stored in the head of the list,
Int Stack : top ()
{
return front->data;
}
Conclusion:
When we say "implementing Stack using Linked List", we mean how we can make a Linked List behave like a Stack, after all, they are all logical entities. So for any data structure to act as a Stack, it should have push() method to add data on the top and pop() method to remove data from the top. Which is exactly what we did and hence accomplished to make a Linked List behave as a Stack.
Circular queues
Circular Queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle and the last position is connected back to the first position to make a circle. It is also called ‘Ring Buffer’
Operations on Circular Queue:

In a normal Queue, we can insert elements until queue becomes full. But once queue becomes full, we can not insert the next element even if there is a space in front of queue.

- Front: Get the front item from queue.
- Rear: Get the last item from queue.
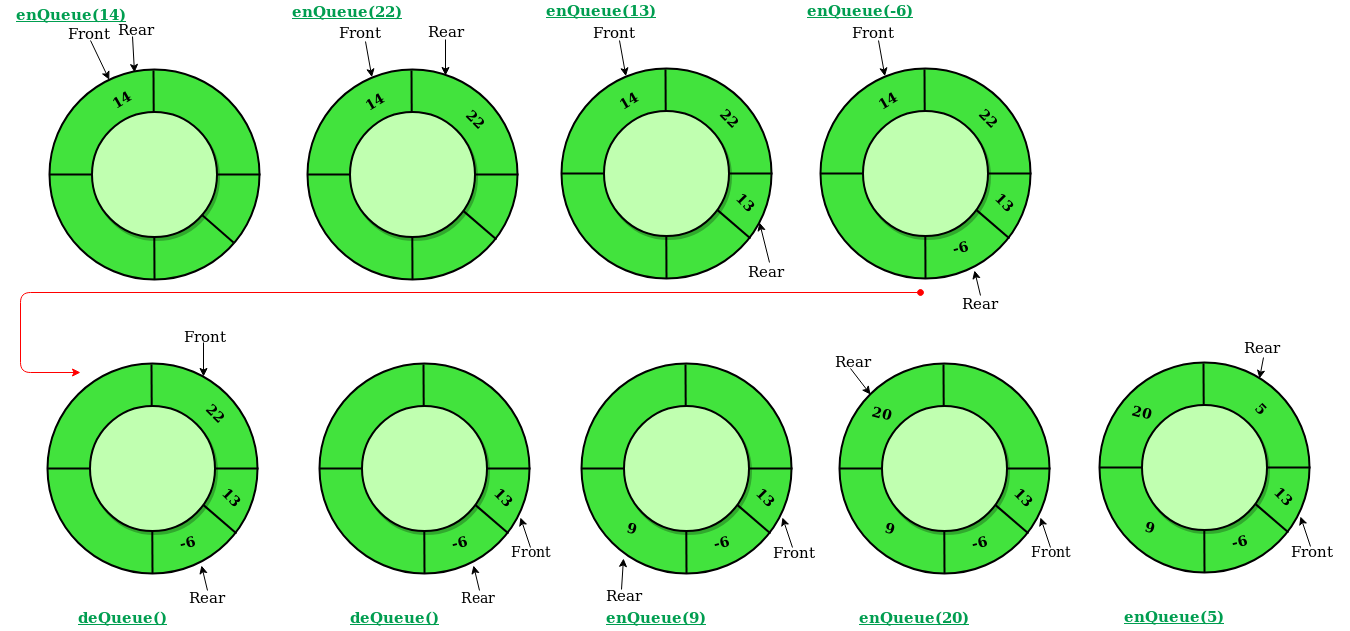
- enQueue(value) This function is used to insert an element into the circular queue. In a circular queue, the new element is always inserted at Rear position.
- Steps:
- Check whether queue is Full – Check ((rear == SIZE-1 && front == 0) || (rear == front-1)).
- If it is full then display Queue is full. If queue is not full then, check if (rear == SIZE – 1 && front != 0) if it is true then set rear=0 and insert element.
- deQueue() This function is used to delete an element from the circular queue. In a circular queue, the element is always deleted from front position.
- Steps:
- Check whether queue is Empty means check (front==-1).
- If it is empty then display Queue is empty. If queue is not empty then step 3
- Check if (front==rear) if it is true then set front=rear= -1 else check if (front==size-1), if it is true then set front=0 and return the element.
Enqueue- adding an element in the queue if there is space in the queue.
Dequeue- Removing elements from a queue if there are any elements in the queue
Front- get the first item from the queue.
Rear- get the last item from the queue.
isEmpty/isFull- checks if the queue is empty or full
Applications of a Circular Queue
Memory management: circular queue is used in memory management.
Process Scheduling: A CPU uses a queue to schedule processes.
Traffic Systems: Queues are also used in traffic systems
Priority Queue
The priority queue is that in which there is an extension of the queue. This is a type of special data structure.
Like ordinary queue, priority queue has same method but with a major difference. In Priority queue items are ordered by key value so that item with the lowest value of key is at front and item with the highest value of key is at rear or vice versa. So we're assigned priority to item based on its key value. Lower the value, higher the priority. Following are the principal methods of a Priority Queue.
Basic Operations
- insert / enqueue − add an item to the rear of the queue.
- remove / dequeue − remove an item from the front of the queue.
Priority Queue Representation

We're going to implement Queue using array in this article. There is few more operations supported by queue which are following.
- Peek − get the element at front of the queue.
- isFull − check if queue is full.
- isEmpty − check if queue is empty.
Insert / Enqueue Operation
Whenever an element is inserted into queue, priority queue inserts the item according to its order. Here we're assuming that data with high value has low priority.

Remove / Dequeue Operation
Whenever an element is to be removed from queue, queue get the element using item count. Once element is removed. Item count is reduced by one.

Basic operations
Basic operations of the priority queue are as follows:
insert / enqueue - adding item to the rear of the queue.
remove / dequeue - remove the item from the front of the queue.
peek - getting the element in the front of the queue.
isfull - it checks if the queue is full.
isEmpty - It checks if the queue is empty.
Applications of priority queue:
It is used in CPU scheduling.
It is used in graph algorithms like - Dijkstra’s shortest path algorithm, prim’s minimum
spanning tree, etc.
It is used in Huffman coding. Huffman coding is used to compress data.
In artificial intelligence.
In operating systems, it is used for load balancing and interrupts handling.
Infix to Postfix Conversion
Any expression can be represented using three types of expressions (Infix, Postfix, and Prefix).
We can also convert one type of expression to another type of expression like Infix to Postfix, Infix to Prefix,
Postfix to Prefix and vice versa.
To convert any Infix expression into Postfix or Prefix expression we can use the following procedure...
To convert any Infix expression into Postfix or Prefix expression we can use the following procedure...
- Find all the operators in the given Infix Expression.
- Find the order of operators evaluated according to their Operator precedence.
- Convert each operator into required type of expression (Postfix or Prefix) in the same order.
Example
Consider the following Infix Expression to be converted into Postfix Expression...
D = A + B * C
- Step 1 - The Operators in the given Infix Expression : = , + , *
- Step 2 - The Order of Operators according to their preference : * , + , =
- Step 3 - Now, convert the first operator * ----- D = A + B C *
- Step 4 - Convert the next operator + ----- D = A BC* +
- Step 5 - Convert the next operator = ----- D ABC*+ =
Finally, given Infix Expression is converted into Postfix Expression as follows...
D A B C * + =
Infix to Postfix Conversion using Stack Data Structure
To convert Infix Expression into Postfix Expression using a stack data structure,
We can use the following steps...
- Read all the symbols one by one from left to right in the given Infix Expression.
- If the reading symbol is operand, then directly print it to the result (Output).
- If the reading symbol is left parenthesis '(', then Push it on to the Stack.
- If the reading symbol is right parenthesis ')', then Pop all the contents of stack
- until respective left parenthesis is poped and print each poped symbol to the result.
- If the reading symbol is operator (+ , - , * , / etc.,), then Push it on to the Stack.
- However, first pop the operators which are already on the stack that have higher
- or equal precedence than current operator and print them to the result.
Example
Consider the following Infix Expression...
( A + B ) * ( C - D )
The final Postfix Expression is as follows...
A B + C D - *
Postfix Expression Evaluation
A postfix expression is a collection of operators and operands in which the operator is placed after the operands
. That means, in a postfix expression the operator follows the operands.
Postfix Expression has following general structure...
Postfix Expression has following general structure...
Operand 1 Operand 2 Operator
ab+
Postfix Expression Evaluation using Stack Data Structure
A postfix expression can be evaluated using the Stack data structure. To evaluate a postfix expression using
Stack data structure we can use the following steps...
- Read all the symbols one by one from left to right in the given Postfix Expression
- If the reading symbol is operand, then push it on to the Stack.
- If the reading symbol is operator (+ , - , * , / etc.,), then perform TWO pop operations and
- store the two popped oparands in two different variables (operand1 and operand2).
- Then perform reading symbol operation using operand1 and operand2 and push result back on to the Stack.
- Finally! perform a pop operation and display the popped value as final result.

No comments:
Post a Comment